|


|
Figure 5.1: |
The direction of the magnetic force exerted on a charged
particle moving in a magnetic field is (a) perpendicular to both B and u and
(b) depends on the charge polarity (positive or negative).
|
|


|
Figure 5.2: |
When a slightly flexible vertical wire is placed in a
magnetic field directed into the page (as denoted by the crosses), it
is (a) not deflected when the current through it is zero, (b) deflected
to the left when I is upward, and (c) deflected to the right when I is
downward.
|
|


|
Figure 5.3: |
In a uniform magnetic field, (a) the net force on a closed
current loop is zero because the integral of the displacement vector
dl over a closed contour is zero, and (b) the force on a line
segment is proportional to the vector between the end point (Fm
= I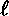 XB). XB).
|
|


|
Figure 5.4: | Semicircular conductor in a uniform field (Example 5-1).
|
|


|
Figure 5.5: |
The force F acting on a circular disk pivoted along
the z-axis generates a torque T = dXF that causes
the disk to rotate.
|
|


|
Figure 5.6: |
Rectangular loop pivoted along the y-axis: (a) front view
and (b) bottom view. The combination of forces F1 and F3
on the loop generates a torque that tends to rotate the loop in a
clockwise direction as shown in (b).
|
|


|
Figure 5.7: |
Rectangular loop in a uniform magnetic field with flux
density B whose direction is perpendicular to the rotation axis
of the loop, but makes an angle 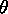 with the loop's surface normal
n-hat. with the loop's surface normal
n-hat.
|
|


|
Figure 5.8: |
Mangetic field dH generated by a current element Idl.
The direction of the field induced at point P is opposite
that induced at point P'.
|
|


|
Figure 5.9: |
(a) The total current crossing the cross section S of the
cylinder is I = integral over S of J dot ds. (b) The total current
flowing across the surface of the conductor is I= integral over l Jsdl.
|
|


|
Figure 5.10: |
Linear conductor of length l carrying a current I. (a)
The field dH at point P due to incremental current element dl.
(b) Limiting angles 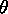 1 and 1 and
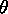 2, each measured between
vector I dl and the vector connecting the end of the conductor
associated with that angle to point P (Example 5-2). 2, each measured between
vector I dl and the vector connecting the end of the conductor
associated with that angle to point P (Example 5-2).
|
|


|
Figure 5.11: |
Pie-shaped loop of radius a carrying a current I (Example
5-3).
|
|


|
Figure 5.12: |
Circular loop carrying a current I (Example 5-4).
|
|


|
Figure 5.13: |
Patterns of (a) the electric field of an electric dipole,
(b) the magnetic field of a magnetic dipole, and (c) the magnetic field
of a bar magnet. Far away from the sources, the field patterns are
similar in all three cases.
|
|


|
Figure 5.14: |
Magnetic forces on parallel current-carrying conductors.
|
|


|
Figure 5.15: |
Whereas (a) the net electric flux through a closed
surface surrounding a charge is not zero, (b) the net magnetic flux
through a closed surface surrounding one of the poles of a magnet is
zero.
|
|


|
Figure 5.16: |
Ampere's law states that the line integral of H
around a closed contour C is equal to the current traversing the
surface bounded by the contour. This is true for contours (a) and (b),
but the line integral of H is zero for the contour in (c) because
the current I (denoted by the circle-enclosed-dot symbol) is not enclosed by the
contour C.
|
|


|
Figure 5.17: |
Infinitely long wire of radius a carrying a uniform
current I along the +z-direction: (a) general configuration showing
contours C1 and C2; (b) cross-sectional view; and (c) a plot of H
versus r (Example 5-5).
|
|


|
Figure 5.18: |
Toroidal coil with inner radius a and outer radius b.
The wire loops usually are much more closely spaced than shown in the
figure (Example 5-6).
|
|


|
Figure 5.19: |
A thin current sheet in the x-y plane carrying a surface
current density Hs = x-hat Js (out of the page) (Example
5-7).
|
|


|
Figure 5.20: |
An electron generates (a) an orbital magnetic moment mo as it rotates around the
nucleus and (b) a spin magnetic moment ms, as it spins about its own axis.
|
|


|
Figure 5.21: |
Comparison of (a) unmagnetized and (b) magnetized domains
in a ferromagnetic material.
|
|


|
Figure 5.22: | Typical hysteresis curve for a ferromagnetic material.
|
|


|
Figure 5.23: | Comparison of hysteresis curves for (a) a hard
ferromagnetic material and (b) a soft ferromagnetic material.
|
|


|
Figure 5.24: |
Bounary between medium 1 with 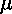 1 and medium 2 with 1 and medium 2 with
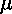 2. 2.
|
|


|
Figure 5.25: |
Magnetic field lines of (a) a lossely wound solenoid and
(b) a tightly wound solenoid.
|
|


|
Figure 5.26: |
Solenoid cross section showing geometry for calculating
H at a point P on the solenoid axis.
|
|


|
Figure 5.27: |
To compute the inductance per unit length of a
two-conductor transmission line, we need to determine the magnetic flux
through the area S between the conductors.
|
|


|
Figure 5.28: |
Cross-sectional view of coaxial transmission line
(Example 5-8).
|
|


|
Figure 5.29: |
Magnetic field lines generated by current I1 in loop 1
linking surface S2 of loop 2.
|
|


|
Figure 5.30: | Toroidal coil with two windings used as a transformer.
|
|


|
Figure 5.31: |
Particle of charge q projected with velocity u into
a medium with a uniform field B perpendicular to u (Problem
5.2).
|
|


|
Figure 5.32: | Configuration of Problem 5.3.
|
|


|
Figure 5.33: | Hinged rectangular loop of Problem 5.4.
|
|


|
Figure 5.34: | Rectangular loop of Problem 5.6.
|
|


|
Figure 5.35: | Current-carrying linear conductor of Problem 5.8.
|
|


|
Figure 5.36: | Configuration of Problem 5.9.
|
|


|
Figure 5.37: | Circular loop next to a linear current (Problem 5.11).
|
|


|
Figure 5.38: | Arrangement for Problem 5.12.
|
|


|
Figure 5.39: | Parallel circular loops of Problem 5.14.
|
|


|
Figure 5.40: | Current loop next to a conducting wire (Problem 5.15).
|
|


|
Figure 5.41: | Parallel conductors supported by strings (Problem 5.16).
|
|


|
Figure 5.42: | A linear current source above a current sheet (Problem
5.17).
|
|


|
Figure 5.43: | Three parallel wires of Problem 5.18.
|
|


|
Figure 5.44: |
Long wire carrying current I2, just above a square loop
carrying I1 (Problem 5.19).
|
|


|
Figure 5.45: | Adjacent magnetic media (Problem 5.30).
|
|


|
Figure 5.46: | Magnetic media separated by the plane x-y=1 (Problem
5.32).
|
|


|
Figure 5.47: | Three magnetic media with parallel interfaces (Problem
5.34).
|
|


|
Figure 5.48: | Loop and wire arrangement for Problem 5.38.
|