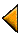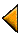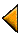|


|
Figure 3.1: |
Vector A= a-hat A has a magnitude A=|A| and unit
vector a-hat=A/A.
|
|


|
Figure 3.2: |
Cartesian coordinate system: (a) base vectors x-hat,
y-hat, and z-hat, and (b) components of vector A.
|
|


|
Figure 3.3: | Vector addition by (a) the parallelogram rule and (b) the
head-to-tail rule.
|
|


|
Figure 3.4: |
Position vector R12=P1P2= R2 -
R1.
|
|


|
Figure 3.5: |
The angle 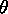 AB is the angle between A and B,
measured from A to B between vector tails. The dot product is positive
if 0 <= AB is the angle between A and B,
measured from A to B between vector tails. The dot product is positive
if 0 <= 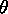 AB < 90o, as in (a), and it is negative if
90o < AB < 90o, as in (a), and it is negative if
90o < 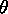 AB <= 180o, as in (b). AB <= 180o, as in (b).
|
|


|
Figure 3.6: |
Cross product AXB points in the direction n-hat,
which is perpendicular to the plane containing A and B and defined by
the right-hand rule.
|
|


|
Figure 3.7: | Geometry for Example 3-1.
|
|


|
Figure 3.8: | Differential length, area, and volume in Cartesian
coordinates.
|
|


|
Figure 3.9: |
Point P (r1, 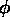 1, z1) in cylindrical coordinates; r1
is the radial distance from the origin in the x-y plane, 1, z1) in cylindrical coordinates; r1
is the radial distance from the origin in the x-y plane, 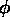 1 is the
angle in the x-y plane measured from the x-axis toward the y-axis, and
z1 is the vertical distance from the x-y plane. 1 is the
angle in the x-y plane measured from the x-axis toward the y-axis, and
z1 is the vertical distance from the x-y plane.
|
|


|
Figure 3.10: | Differential areas and volume in cylindrical
coordinates.
|
|


|
Figure 3.11: | Geometry of Example 3-3.
|
|


|
Figure 3.12: | Cylindrical surface of Example 3-4.
|
|


|
Figure
3.13: |
Point P(R1, 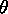 1, 1,
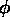 1) in spherical coordinates. 1) in spherical coordinates.
|
|


|
Figure 3.14: | Differential volume in spherical coordinates.
|
|


|
Figure 3.15: | Spherical strip of Example 3-5.
|
|


|
Figure
3.16: |
Interrelationships between Cartesian coordinates (x, y,
z) and cylindrical coordinates (r, 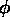 , z). , z).
|
|


|
Figure
3.17: |
Interrelationships between base vectors (x-hat, y-hat) and
(r-hat, 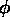 -hat). -hat).
|
|


|
Figure
3.18: |
Interrelationships between (x,y,z) and (R,
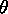 , , 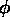 ). ).
|
|


|
Figure
3.19: |
Differential distance vector dl between points P1
and P2.
|
|


|
Figure
3.20: |
Flux lines of the electric field E due to a positive
charge q.
|
|


|
Figure
3.21: |
Flux lines of a vector field E passing through a
differential rectangular parallelepiped of volume
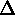 v = v =
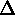 x x
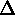 y y
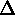 z. z.
|
|


|
Figure 3.22: |
Circulation is zero for the uniform field in (a), but it
is not zero for the azimuthal field in (b).
|
|


|
Figure 3.23: |
The direction of the unit vector n-hat is along the thumb
when the other four fingers of the right hand follow dl.
|
|


|
Figure 3.24: | Geometry for Example 3-12.
|
|


|
Figure 3.25: |
Arrow representation for vector field E=r-hat r (Problem
3.18).
|
|


|
Figure 3.26: | Contours for (a) Problem 3.43 and (b) Problem 3.44.
|
|


|
Figure 3.27: | Contour paths for (a) Problem 3.45 and (b) Problem 3.46.
|